An introduction to IGA

Kiwi!3D, a new plug-in for Grasshopper and Rhinoceros, is based on Isogeometric Analysis (IGA) in order to directly integrate structural analysis into CAD. IGA is a subgroup of Finite Element Methods. Its special characteristic lies in the usage of Non-Uniform Rational B-Splines (NURBS) as basis functions for the Finite Elements, which are commonly used for the geometry description in CAD. Hence, a complete reparametrization (meshing) of CAD models for analysis is avoided.

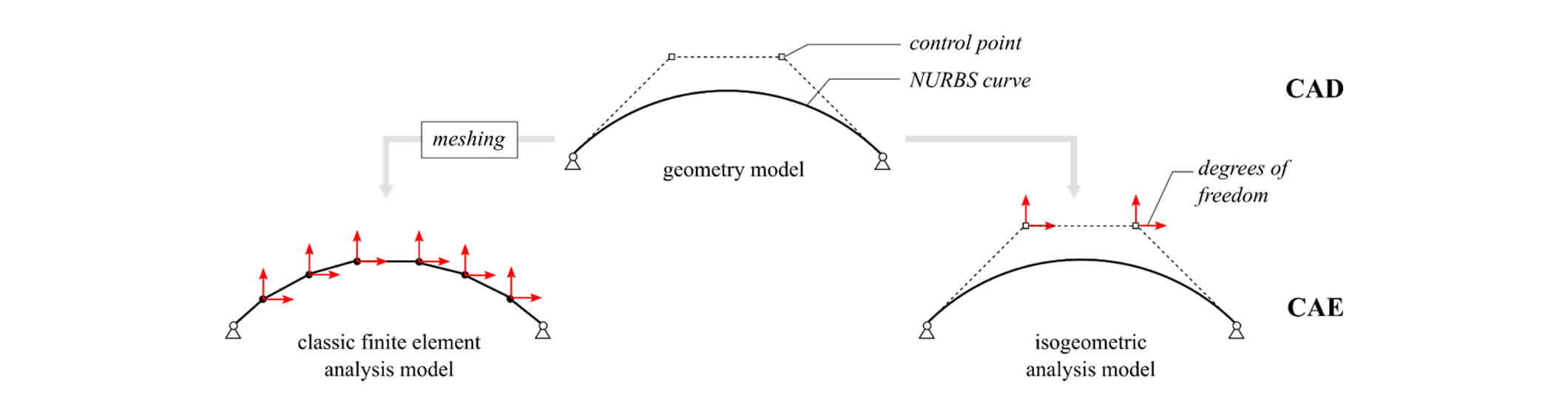
The degrees of freedom do not lie on the surface of the element but on the control points of the geometry. The refinement can be done at every stage before and during the analysis without changing the geometry. The applied FEM-kernel is Carat++, which is proprietary research from the Chair of Structural Analysis at the Technical University of Munich. Kiwi!3D works as interface for pre- and postprocessing within Rhino/Grasshopper.

Kiwi!3D provides access to advanced features for:

Non-linear Analysis
Form Finding
Construction Stage Simulation (consideration of stress history in consecutive simulation tasks)
Cutting Pattern Generation (under construction)

The following isogeometric element types are available within Kiwi!3D:

Kichhoff-Love Shell Element
Membrane Element
Bernoulli Beam 3D Element
Cable Element
Coupling Elements (Translations, Rotations)

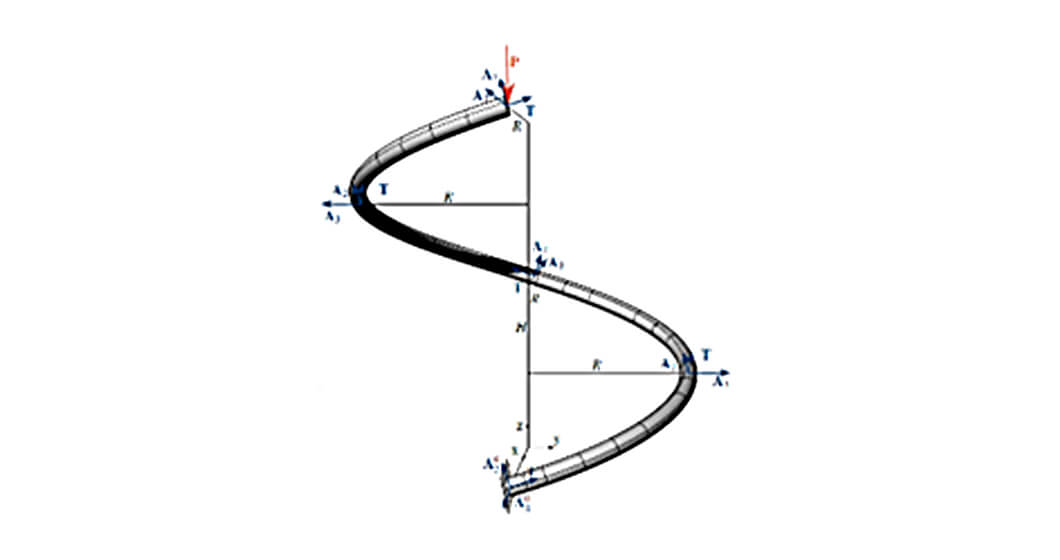
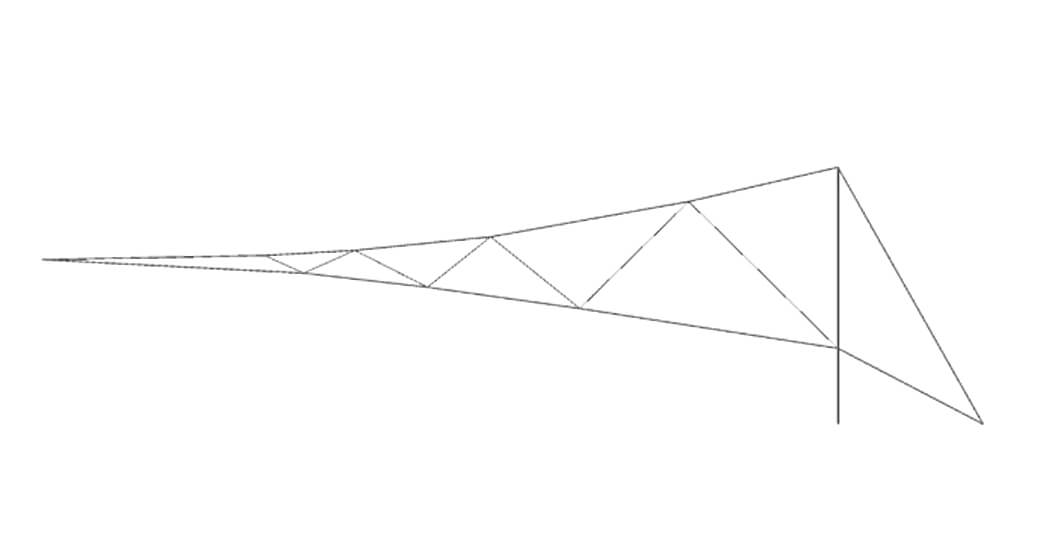
Further advantages of using IGA in the design of these kind of structures can be seen in the independence of the parametrization for boundary conditions such as loads, supports and coupling entities. All CAD features are available e.g. for the derivation of additional structural members. The method-inherent ability to consistently represent the whole sequence of construction stages during the design process, without losing or having to approximate stresses or displacements, enables a detailed evaluation and enhanced design. The continuous basis functions allow a smooth representation of geometry and results.

Examples

"Isoropia", Danish Pavillion, Venice Biennale 2018 (Architects: CITA, Copenhagen)

Bending Active Textile Hybrid Structure (Lienhard, Hafen City University Hamburg, 2017)

Form Finding for Membrane Roof, Velden (Architects: Kugel Architekten)

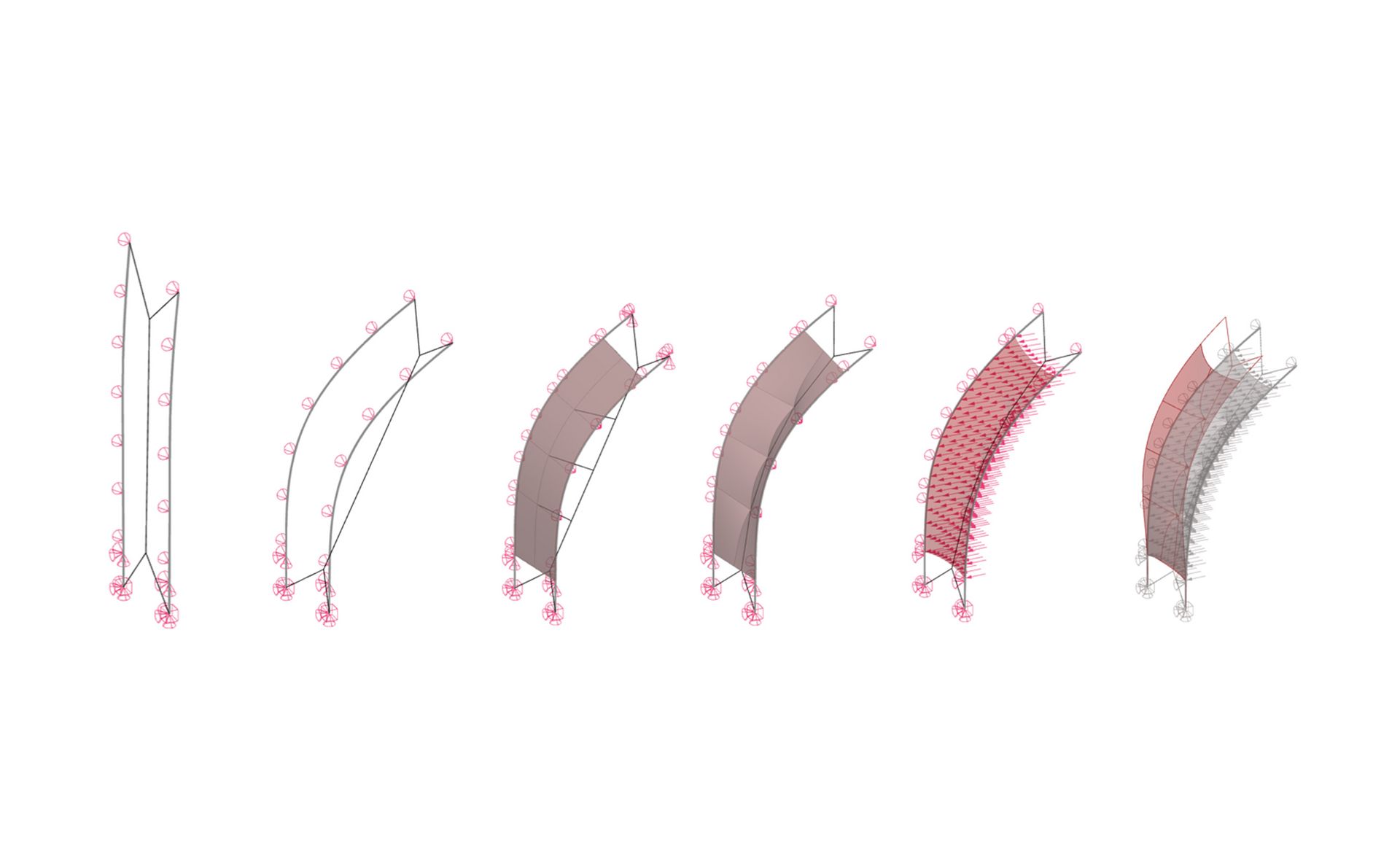
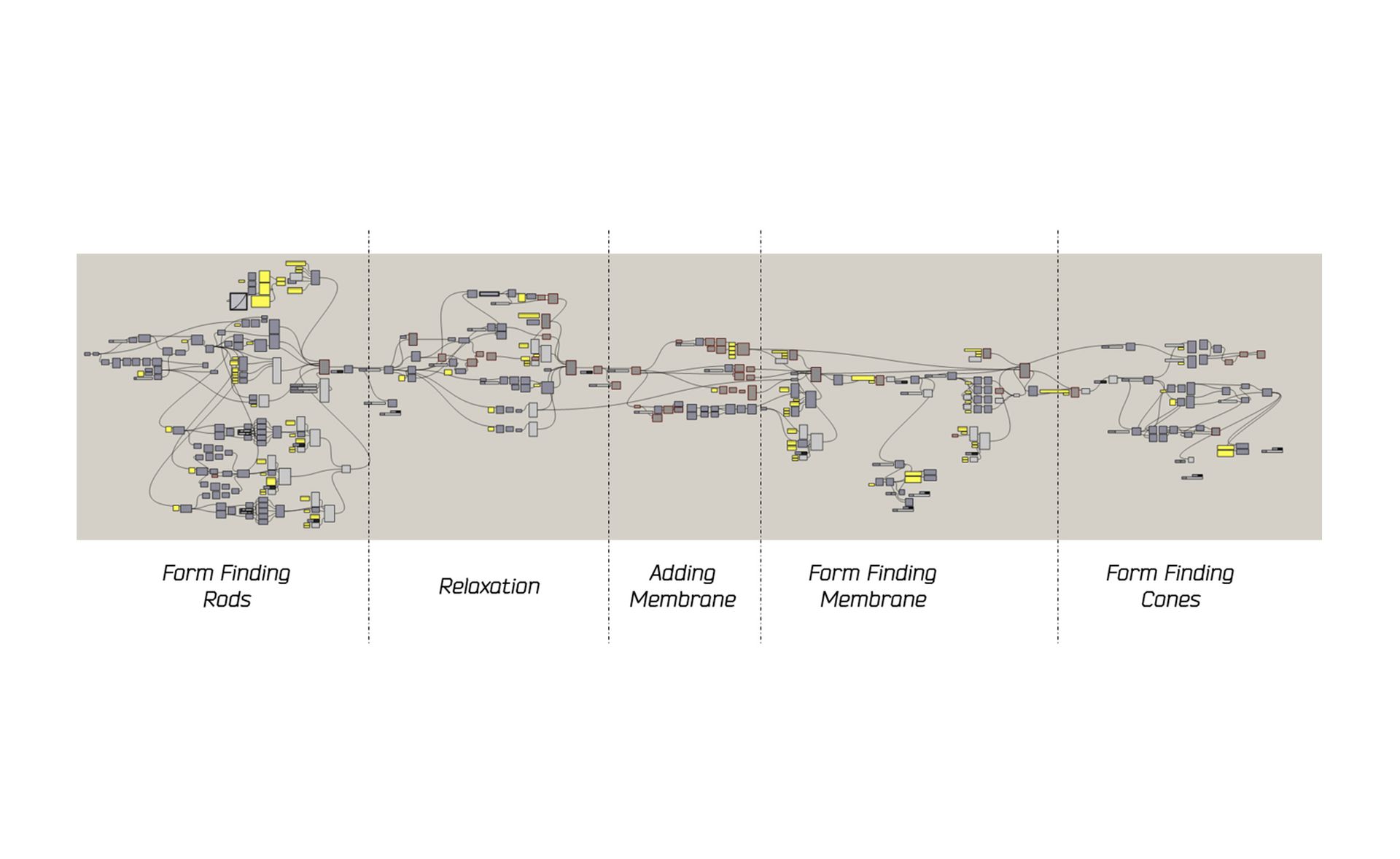
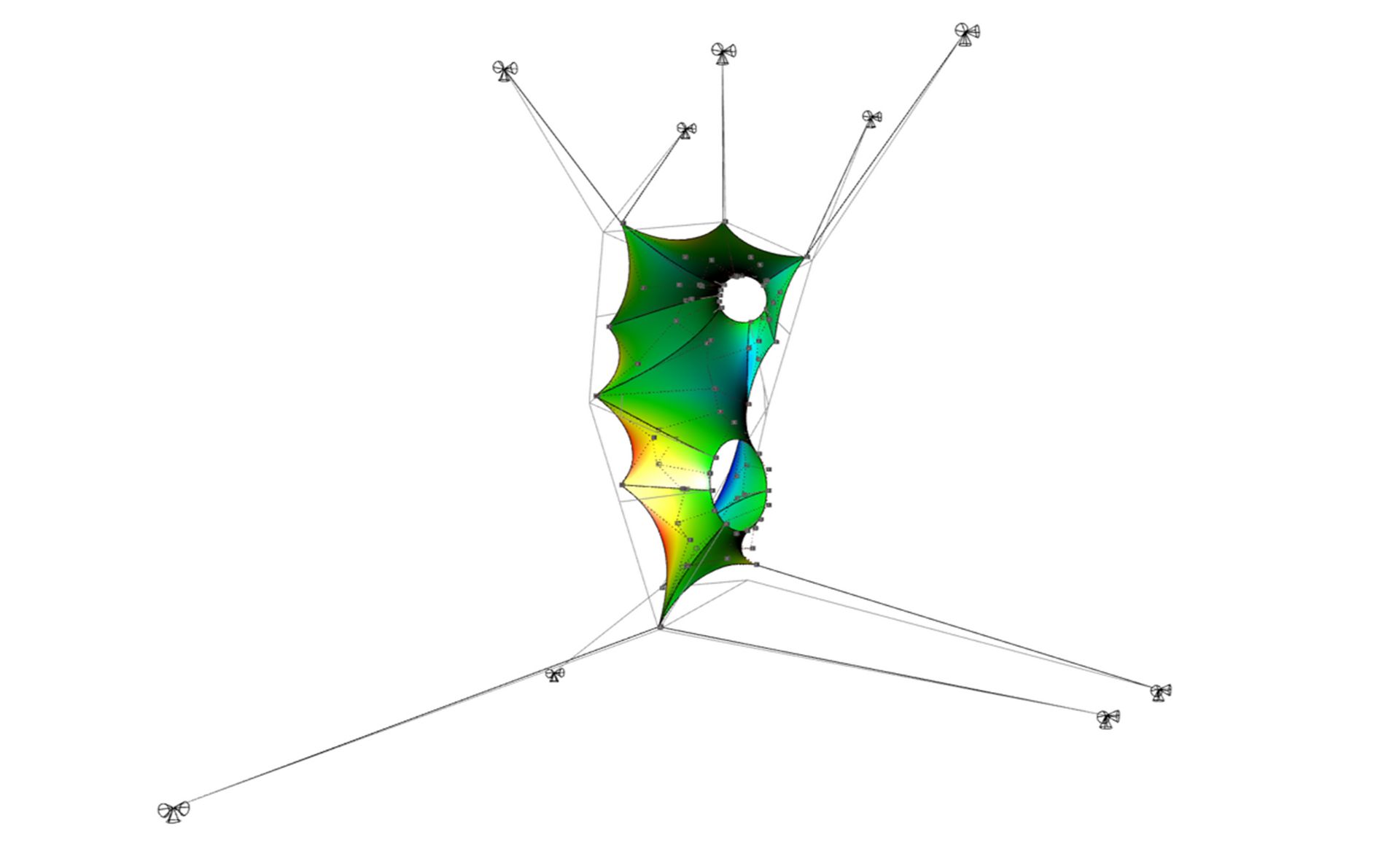
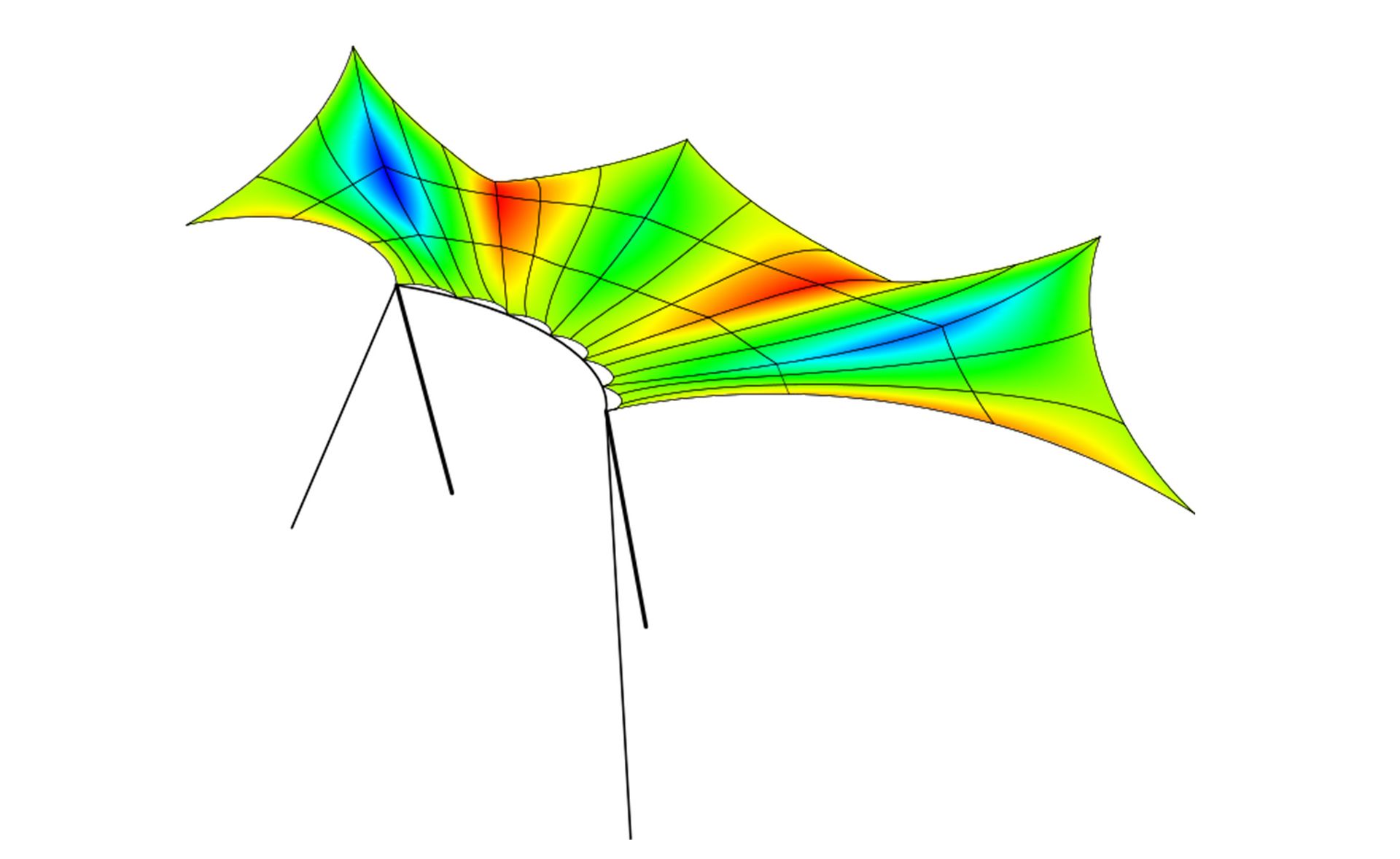
References

Related Literature:

Isogeometric Analysis and Shape Optimal Design of Shell Structures, Dissertation Josef M. Kiendl, 2010

Apostolatos, A.; Schmidt, R.; Wüchner, R.; Bletzinger, K.-U.: A Nitsche-type formulation and comparison of the most common domain decomposition methods in isogeometric analysis. International Journal for Numerical Methods in Engineering 97 (7), 2014, 473-504

Bauer, A. M.; Wüchner, R.; Bletzinger, K.-U.; “Isogeometric Analysis for Staged Construction within Lightweight Design,” in VIII International Conference on Textile Composites and Inflatable Structures, 2017.

Bauer, A. M., Längst; P.; Wüchner, R.; Bletzinger, K.-U.; “Isogeometric Analysis for Modeling and Simulation of Building Processes,” in Proceedings of the IASS Annual Symposium 2017 “Interfaces: architecture. engineering. science,” 2017.

Bauer, A.M.; Breitenberger, M.; Philipp, B.; Wüchner, R.; Bletzinger, K.-U.: Nonlinear isogeometric spatial Bernoulli Beam. Computer Methods in Applied Mechanics and Engineering 303, 2016, 101-127

Breitenberger, M.: CAD-Integrated Design and Analysis of Shell Structures, Dissertation, 2016

Breitenberger, M.; Apostolatos, A.; Philipp, B.; Wüchner, R.; Bletzinger, K.-U.: Analysis in computer aided design: Nonlinear isogeometric B-Rep analysis of shell structures. Computer Methods in Applied Mechanics and Engineering 284, 2015, 401—457

Hughes, T. J. R.; Cottrell, J. A.; Bazilevs, Y.; “Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement,” Comput. Methods Appl. Mech. Eng., vol. 194, no. 39–41, pp. 4135–4195, Oct. 2005.

Längst, P. ; Bauer, A. M.; Michalski, A. ; Lienhard, J.; “The Potentials of Isogeometric Analysis Methods in Integrated Design Processes,” in Proceedings of the IASS Annual Symposium 2017 “Interfaces: architecture. engineering. science,”2017.

Philipp, B.; Breitenberger, M.; D’Auria, I.; Wüchner, R.; Bletzinger, K.-U.: Integrated design and analysis of structural membranes using the Isogeometric B-Rep Analysis. Computer Methods in Applied Mechanics and Engineering 303, 2016, 312-340

Philipp, B.: Methodological Treatment of Non-linear Structural Behavior in the Design, Analysis and Verification of Lightweight Structures, Dissertation, 2017

Research Project Technische Universität München:
www.st.bgu.tum.de/forschung/drittmittelprojekte/iga-in-leichtbauplanung/

Sponsorship

The development of Kiwi!3D is funded within the “Zentrales Innovationsprogramm Mittelstand” of the “Bundesministerium für Wirtschaft und Energie” (BMWi, funding code ZF4200001BZ6).